7laha is a smart example to learn more.
Two plates(5*20) are welded in continuous way with an extruded beam has the shown cross section and a uniform thickness of 3mm and they carry the loads as shown.
Step 1
Ra+Rc=(6.2+3*0.36)=7.28 KN
MOMENT AROUND C =0
SO 3*0.18*RA=7.28*0.18 RA=2.4 KN
A cording to rod fg and the similar rod the length of the rod from the triangle
We divide the trapezoid into 4 rods
Where i=second moment of area.
Q=first moment of area
b=thickness of part is cut.
Step 2:
Y`=SUM (A*Y)/SUM A
Look to datum position in section figure.
Y`=[(20*5)*38+2*(34*3)*(30/2 +3/2 + 5/2) +(60*3)*(30+1.5+2.5)+(28*3)*(1.5+2.5)]
÷[(20*5)+(2*34*3)+(60*3)+(28*3)+(20*5)]
=24.88 mm =25mmStep 3:
Calculation of i=(b(h^3)/12 +A(d^2) )
I for
Upper plate=((20*(5^3)/12 +(20*5)*((38-25)^2))
Upper rod =(60*(3^3)/12 +(60*3)*((34-25)^2))
How we can get I for fg rod?
b`=b/cosɵ
b`=3/(30/34)=3.4mm and h=30 mm not 34mm(deal with it now as a vertical rectangular)
For lower rod of trapezoid i=((28*(3^3)/12 +(28*3*(25-4)^2)
For lower plate i=((20*(5^3)/12 +(20*5*(25-2.5)^2)
I total =14.2 *(10^-8) m^4
Q=A*Y`
Q AT b will include the cut rectangular and the upper plate .
For symmetry we will cut at two edges at distance 25 mm from each edge=10mm width for the cut part.
The thickness of cut part=3mm(trapezoid thickness)
Q=(10*3*(34-25))+(20*5*13)=1570*(10^-9) m^3
b=2*3=6mm
sh.stat b=RA*Q/I*b*2
=(2.4*1000)*(1570*10^-9) /(14.2*6*10^-11)*2
2.21MPA




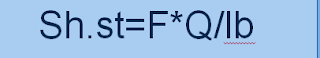

good work
ReplyDelete