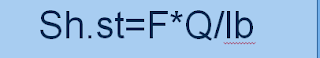30 May 2011
chapter(7)_transformation of beams (1)
by>> www.efunda.com
Mohr's Circle
Introduced by Otto Mohr in 1882, Mohr's Circle illustrates principal stresses and stress transformations via a graphical format,
The two principal stresses are shown in red, and the maximum shear stress is shown in orange. Recall that the normal stesses equal the principal stresses when the stress element is aligned with the principal directions, and the shear stress equals the maximum shear stress when the stress element is rotated 45° away from the principal directions.
As the stress element is rotated away from the principal (or maximum shear) directions, the normal and shear stress components will always lie on Mohr's Circle.
Mohr's Circle was the leading tool used to visualize relationships between normal and shear stresses, and to estimate the maximum stresses, before hand-held calculators became popular. Even today, Mohr's Circle is still widely used by engineers all over the world.
Derivation of Mohr's Circle
To establish Mohr's Circle, we first recall the stress transformation formulas for plane stress at a given location,
Using a basic trigonometric relation (cos22q + sin22q = 1) to combine the two above equations we have,
This is the equation of a circle, plotted on a graph where the abscissa is the normal stress and the ordinate is the shear stress. This is easier to see if we interpret sx and sy as being the two principal stresses, and txy as being the maximum shear stress. Then we can define the average stress, savg, and a "radius" R (which is just equal to the maximum shear stress), 
The circle equation above now takes on a more familiar form,
The circle is centered at the average stress value, and has a radius R equal to the maximum shear stress, as shown in the figure below,
Cylindrical Pressure Vessel
Consider a cylindrical pressure vessel with radius r and wall thickness t subjected to an internal gage pressure p.
The coordinates used to describe the cylindrical vessel can take advantage of its axial symmetry. It is natural to align one coordinate along the axis of the vessel (i.e. in the longitudinal direction). To analyze the stress state in the vessel wall, a second coordinate is then aligned along the hoop direction.
With this choice of axisymmetric coordinates, there is no shear stress. The hoop stress sh and the longitudinal stress sl are the principal stresses.
To determine the longitudinal stress sl, we make a cut across the cylinder similar to analyzing the spherical pressure vessel. The free body, illustrated on the left, is in static equilibrium. This implies that the stress around the wall must have a resultant to balance the internal pressure across the cross-section. 
Applying Newton's first law of motion, we have, 
and <this strees is a n axial stress&get;
· To determine the hoop stress sh, we make a cut along the longitudinal axis and construct a small slice as illustrated on the right.
The free body is in static equilibrium. According to Newton's first law of motion, the hoop stress yields,
chapter (7)_transformation of plane stress (2)
By www.efunda.com
Given the stresses at a space point in the body, sx, sy, and txy, this calculator computes the stresses of the same space point in a rotated coordinate system, sx', sy', and tx'y'.
Equations behind the Calculator
The following coordinate transformation equations were used,
principale stresses
Given the stress components sx, sy, and txy, this calculator computes the principal stresses s1, s2, the principal angle qp, the maximum shear stress tmax and its angle qs. It also draws an approximate Mohr's cirlce for the given stress state.
The Mohr's circle associated with the above stress state is similar to the following figure. However, the exact loaction of the center sAvg, the radius of the Mohr's circle R, and the principal angle qp may be different from what are shown in the figure.
Equations behind the Calculator
The formulas used in this calculator are,
chapter(7)_transformation of plane stress (2)
Calculator Introduction of the stresses
Given the stresses at a space point in the body, sx, sy, and txy, this calculator computes the stresses of the same space point in a rotated coordinate system, sx', sy', and tx'y'.
Equations behind the Calculator
The following coordinate transformation equations were used,
principale stresses
Given the stress components sx, sy, and txy, this calculator computes the principal stresses s1, s2, the principal angle qp, the maximum shear stress tmax and its angle qs. It also draws an approximate Mohr's cirlce for the given stress state.
The Mohr's circle associated with the above stress state is similar to the following figure. However, the exact loaction of the center sAvg, the radius of the Mohr's circle R, and the principal angle qp may be different from what are shown in the figure.
Equations behind the Calculator
The formulas used in this calculator are,
Chapter(7)_ Transformation of plane stress
Mohr's Circle
Introduced by Otto Mohr in 1882, Mohr's Circle illustrates principal stresses and stress transformations via a graphical format,
The two principal stresses are shown in red, and the maximum shear stress is shown in orange. Recall that the normal stesses equal the principal stresses when the stress element is aligned with the principal directions, and the shear stress equals the maximum shear stress when the stress element is rotated 45° away from the principal directions.
As the stress element is rotated away from the principal (or maximum shear) directions, the normal and shear stress components will always lie on Mohr's Circle.
Mohr's Circle was the leading tool used to visualize relationships between normal and shear stresses, and to estimate the maximum stresses, before hand-held calculators became popular. Even today, Mohr's Circle is still widely used by engineers all over the world.
Derivation of Mohr's Circle
To establish Mohr's Circle, we first recall the stress transformation formulas for plane stress at a given location,
Using a basic trigonometric relation (cos22q + sin22q = 1) to combine the two above equations we have,
This is the equation of a circle, plotted on a graph where the abscissa is the normal stress and the ordinate is the shear stress. This is easier to see if we interpret sx and sy as being the two principal stresses, and txy as being the maximum shear stress. Then we can define the average stress, savg, and a "radius" R (which is just equal to the maximum shear stress),
The circle equation above now takes on a more familiar form,
The circle is centered at the average stress value, and has a radius R equal to the maximum shear stress, as shown in the figure below,
Cylindrical Pressure Vessel
Consider a cylindrical pressure vessel with radius r and wall thickness t subjected to an internal gage pressure p.
The coordinates used to describe the cylindrical vessel can take advantage of its axial symmetry. It is natural to align one coordinate along the axis of the vessel (i.e. in the longitudinal direction). To analyze the stress state in the vessel wall, a second coordinate is then aligned along the hoop direction.
With this choice of axisymmetric coordinates, there is no shear stress. The hoop stress sh and the longitudinal stress sl are the principal stresses.
To determine the longitudinal stress sl, we make a cut across the cylinder similar to analyzing the spherical pressure vessel. The free body, illustrated on the left, is in static equilibrium. This implies that the stress around the wall must have a resultant to balance the internal pressure across the cross-section.
Applying Newton's first law of motion, we have,
and <this strees is a n axial stress&get;
· To determine the hoop stress sh, we make a cut along the longitudinal axis and construct a small slice as illustrated on the right.
The free body is in static equilibrium. According to Newton's first law of motion, the hoop stress yields,
29 May 2011
Structural Analysis I lectures (on youtube)
Structural Analysis I lectures (on youtube)
Beam Deflection (Chapter9)
Shear Stresses(Chapter 6)
Principle Stresses (Chapter 7)
special thanks , to media team ..
21 May 2011
16 May 2011
my house
only creative people can make their dreams and live in them as a real life. today let us imagine where do we want to live in?
i want to live in a house on small island has:
1-garden with beautiful fruits.
2-roof like bird nest.
3-mirror from diamond.
4-bed on the water.
5-horses park has many horses.
6-park for dolphins.
7-touch screens on the wall to manage my business.
8-seat can have place to store my laptop.
9- moving seat.
10-moving ceramics on the floor.
11- good smell from the wall.
12-entering the house by my family DNA.
13-helicopter landing place on the roof.
14-pc write my orders and send them by e-mile.
there are many pictures for wonderful houses.
09 May 2011
Pen
i suggest some ideas to develop our pen , and i wait your ideas to write by click on the upper advertisement. i can image new pen in these forms:
1-pen with alarm to help me get up or to make some work.
2-pen with ball shape.
3-pen can fly by filled it with helium.
4-pen with mirror.
5-pen with radio or calculator .
6-pen when fall i know.
7-pen with good perfume.
8-pen cannot be broken.
05 May 2011
Smart example on shear stress.
7laha is a smart example to learn more.
Two plates(5*20) are welded in continuous way with an extruded beam has the shown cross section and a uniform thickness of 3mm and they carry the loads as shown.
Step 1
Ra+Rc=(6.2+3*0.36)=7.28 KN
MOMENT AROUND C =0
SO 3*0.18*RA=7.28*0.18 RA=2.4 KN
A cording to rod fg and the similar rod the length of the rod from the triangle
We divide the trapezoid into 4 rods
Where i=second moment of area.
Q=first moment of area
b=thickness of part is cut.
Step 2:
Y`=SUM (A*Y)/SUM A
Look to datum position in section figure.
Y`=[(20*5)*38+2*(34*3)*(30/2 +3/2 + 5/2) +(60*3)*(30+1.5+2.5)+(28*3)*(1.5+2.5)]
÷[(20*5)+(2*34*3)+(60*3)+(28*3)+(20*5)]
=24.88 mm =25mm
Step 3:
Calculation of i=(b(h^3)/12 +A(d^2) )
I for
Upper plate=((20*(5^3)/12 +(20*5)*((38-25)^2))
Upper rod =(60*(3^3)/12 +(60*3)*((34-25)^2))
How we can get I for fg rod?
b`=b/cosɵ
b`=3/(30/34)=3.4mm and h=30 mm not 34mm(deal with it now as a vertical rectangular)
For lower rod of trapezoid i=((28*(3^3)/12 +(28*3*(25-4)^2)
For lower plate i=((20*(5^3)/12 +(20*5*(25-2.5)^2)
I total =14.2 *(10^-8) m^4
Q=A*Y`
Q AT b will include the cut rectangular and the upper plate .
For symmetry we will cut at two edges at distance 25 mm from each edge=10mm width for the cut part.
The thickness of cut part=3mm(trapezoid thickness)
Q=(10*3*(34-25))+(20*5*13)=1570*(10^-9) m^3
b=2*3=6mm
sh.stat b=RA*Q/I*b*2
=(2.4*1000)*(1570*10^-9) /(14.2*6*10^-11)*2
2.21MPA
Subscribe to:
Posts (Atom)